Category theory has traditionally always been a matter of great contention. Since its inception, it has been applied almost everywhere across mathematics. Most notably it is often credited for having the greatest impact in the development of homological algebra and later algebraic topology & geometry. While its impact on mathematics as a whole is indeed seminal, a significant part of the mathematical community (largely that of the constructive variety) still insists that this impact is purely cosmetic and merits no real value.

Average category theorist, according to analysts and constuctivists.

What is a category, anyway?

The notion of the category seeks to generalize the intuitive idea that a lot of abstract constructions in mathematics are “essentially” the same. The first step for achieving this is to precisely define what a “category” is. To that end, the formal definition, as given in most treatments of the theory goes as follows.

Definition (Category) A category $\mathcal{C}$ is a collection (3-tuple) consisting of

• A class $\mathrm{Ob}(\mathcal{C})$ of "objects".
• A class $\mathrm{Hom}(\mathcal{C})$ of "morphisms", or maps between the objects. Here, $\mathrm{Hom}(a, b)$ is used to denote the subclass of $\mathrm{Hom}(\mathcal{C})$ which consists only of maps $f: a \to b$.
• A binary operation $\circ: \mathrm{Hom}(a, b) \times \mathrm{Hom}(b, c) \to \mathrm{Hom}(a, c)$.

such that the following two properties are satisfied

1. (Associativity) If $f: a \to b$, $g: b \to c$ and $h: c \to d$ then $$h \circ (g \circ f) = (h \circ g) \circ f$$
2. (Identity) For every object $x$, there exists a morphism $1_x: x \to x$ called the identity morphism for $x$, such that for every morphism $f: a \to b$ we have $f = 1_b \circ f = f \circ 1_a$.

This definition, altough all-encompassing, is probably not very enlightening. Indeed, there exists a very visual way of thinking about categories, that is, treating elements of $\mathrm{Hom}(\mathcal{C})$ as if they were arrows and elements of $\mathrm{Ob}(\mathcal{C})$ as if they were nodes. In this way, we get a directed graph of sorts, something like the following.

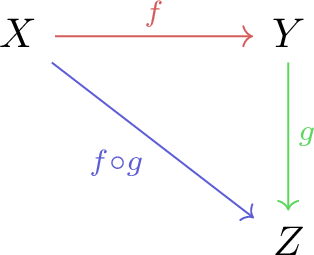
This is of course a category on the objects $X, Y, Z$, with morphisms $f$ and $g$. What exactly these objects are, or how exactly the morphisms transform them is irrelevant. Category theory is concerned only with the broader picture. $X, Y$ and $Z$ could be sets, groups, rings, fields, vector spaces, topological spaces, manifolds, or anything else that admits mappings to and from it really. This seems far too general to be interesting or useful in any way. Doesn’t it? What is the value in this then? Why did we define all this stuff?

Commutative diagrams and functors

Before getting into the actual reason why category theory is in fact useful, it is imperative that we mention some more preliminary definitions. After all, this short treatment is meant to be completely self contained. The first of these, the commutative diagram, is nothing more than a notational convenience. It allows us to elegantly express many properties of morphisms in a visual way, aiding the reader and ourselves. In short, without getting into formalities, a diagram in category theory is a directed graph, whose vertices are the objects and the edges are the morphisms between them (like the graph above). We say that a diagram commutes or is commutative, when all paths that have the same source and endpoints lead to the same result. In other words, if we have

\[x\xrightarrow{f_1} a_1\xrightarrow{f_2} a_2\xrightarrow{f_3} \cdots \xrightarrow{f_n} y\]

and

\[x\xrightarrow{g_1} b_1\xrightarrow{g_2} b_2\xrightarrow{g_3} \cdots \xrightarrow{g_n} y\]

then necessarily $f_1 \circ \cdots \circ f_n = g_1 \circ \cdots \circ g_n$. A functor, on the other hand, is a mapping between two categories, analogous to a homomorphism in algebra, a homeomorphism in topology, or a linear transformation in linear algebra. In particular, we have the following definition.

Definition (Functor) a functor $F: \mathcal{C} \to \mathcal{D}$ between two categories $\mathcal{C}$ and $\mathcal{D}$ is a mapping that

• Associates each object $X$ of $\mathcal{C}$ to the object $F(X)$ in $\mathcal{D}$.
• Associates each morphism $f$ of $\mathcal{C}$ to the morphism $F(f)$ in $\mathcal{D}$, such that the following two conditions are satisfied.
  1. $F(1_X) = 1_{F(X)}$ for every object $X$ of $\mathcal{C}$.
  2. $F(g \circ f) = F(g) \circ F(f)$ for all morphisms $f: X \to Y$ and $g: Y \to Z$ in $\mathcal{C}$.

As can probably be discerned by the astute reader, the second condition is the heart of this definition, the thing that makes the existence of a functor between two categories “noteworthy”. Indeed, categories that are related by a functor are similar in the sense that all commutative diagrams are transformed between them, as well as all isomorphisms (bijective morphisms). Having these two new ideas in mind, we can move forward to defining the main objects of our interest.

Naturality and natural transformations

A very often quoted excerpt from Categories for the Working Mathematician, in many ways the founding text and defining treatise of category theory, is “I didn’t invent categories to study functors; I invented them to study natural transformations”. “I”, of course, is referring to Saunders Mac Lane, one of the co-discoverers of the theory and author of the book referenced above.

Wrong Mac Lane.

This particular concept is a bit more abstract than the ones presented above, so I believe some motivation is in order. Following Category Theory in Context (another great book), I will present the following simplified example. If you happen not to be so comfortable with linear algebra, you are encouraged to skip straight to the definition presented below.

Example (Dual vector space) Consider a field $\mathbb{k}$ and let $\mathbf{Vect}_\mathbb{k}$ be the category of all $\mathbb{k}$-vector spaces, with linear transformations as morphisms. Let $V$ be an object in this category. Its dual vector space, $V^*$, is defined as the set of all linear maps $V \to \mathbb{k}$ ($\mathbb{k}$ is too a vector space over itself). These vector spaces turn out to be isomorphic, which we can prove by showing that they have the same dimension (these are equivalent statements). The concrete way to do it, is to explicitly construct a basis for $V^*$. Choosing a basis $e_1, e_2, \dots, e_n$ of $V$, we let $$ e_i^*(e_j) = \begin{cases} 1,\; i = j \\ 0,\; i \ne j \end{cases} $$ It can be routinely checked that $e_1^*, e_2^*, \dots, e_n^*$ is a basis of $V^*$, and so we're done. This construction is considered ugly, or unnatural, because in order to carry it out we had to make a choice of basis, essentially forcing ourselves to "concretify" the vector space, no longer having it in mind as something general and abstract. Of course, there is a functor denoted by $(-)^*: \mathbf{Vect}_{\mathbb{k}} \to \mathbf{Vect}_{\mathbb{k}}$ taking whatever isomorphism $V \cong V^*$, to the whatever isomorphism $V^* \cong V^{**}$. The composite isomorphism of course establishes an isomorphism $V \cong V^{**}$. It turns out that there is a natural, perhaps canonical as it is often called, construction of this isomorphism. Define the evaluation map, such that for any $v \in V$, $$\mathrm{eval}_v(f) \equiv f(v),\; V^* \to V$$ As fate often has it, it turns out that $v \mapsto \mathrm{eval}_v$ defines our desired isomorphism. It can be seen why this construction would be considered more natural, since it required no choice of basis! We simply defined a single function that works for every single basis in $V$.

The above example can be generalised for any category and will be an indispensable tool for any of our further studying. Without any further ado, we define the natural transformation.

Definition (Natural transformation) Let $\mathcal{C}$ and $\mathcal{D}$ be categories and $F, G: \mathcal{C} \to \mathcal{D}$ be functors. A natural transformation $\eta: F \to G$, is a collection of morphisms. In particular:

• It assigns an arrow (morphism) $\eta_X: F(X) \to G(X)$ for every object $X$ in $\mathcal{C}$. This morphism is called the component of $\eta$ at $X$.
• Components must be such that, for every morphism $f: X \to Y$ the following diagram commutes:

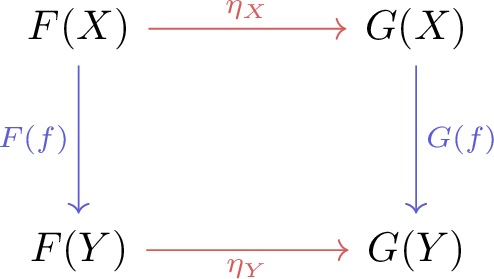
In reality, all natural transformations really “do”, is transform a functor between two categories into another, in a nice way. In the example above, the “double dual” operation, namely $V \to V^{**}$ is a functor, and the maps defined transform the identity functor, $\mathrm{Id}$ to the double dual functor. We can now apply this mechanism to describe similar constructions, transforming long, boring calculations, to “$X$ is naturally isomorphic to $X^\mathrm{op}$” (here, “isomorphic” means that all the components in the transformation are isomorphisms).

Universal morphisms

Consider the following problem: you have arrived at two different constructions for two seemingly distinct objects. Thing is, you do suspect that the constructions yield more-or-less the exact same thing, but are unable to prove it so. What now, Sherlock? Ah, but of course! Category theory has the answer! The “invariant” (of sorts) you’re looking for, is what is known in the lingo as a “universal property”. The idea is that you can reduce the problem to showing that the two constructed objects satisfy the same such property, thus characterising them up to isomorphism. All these words may mean nothing to you right now, so I’ll try to illuminate things by being a bit more precise. We will first give a very superficial definition for the namesake of this section, the universal morphism.

Definition (Universal morphism) Let $\mathcal{C}, \mathcal{D}$ be two categories and $F: \mathcal{C} \to \mathcal{D}$ be a functor between them. Let $A$ and $A'$ be objects of $\mathcal{C}$, denote by $X$ an object in $\mathcal{D}$ and let $h: A \to A'$ a morphism. A universal morphism from $X$ to $F$ is a tuple $(A, u: X \to F(A))$ that satisfies the universal property. Namely, it is the unique such tuple, so that the following diagram commutes:

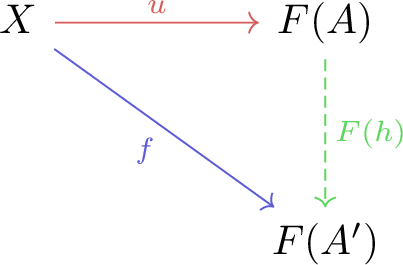
In order to demonstrate the usefulness of this abstract definition, we will follow the classical construction of the equaliser in $\mathbf{Set}$. Stated colloquially, the equaliser, $\mathrm{Eq}(f, g)$ for a set $X$, is defined for two functions $f, g: X \to X$ as

\[\mathrm{Eq}(f, g) = \{x \in X : f(x) = g(x)\}\]

this definition may work fine for sets, but in order to motivate the categorical machinery, we will try to give a definition through the universal morphism. Indeed, let’s consider all the properties that $\mathrm{Eq}$ satisfies. Throughout, let \(X = \{x_1, x_2, \dots, x_n\}\) be a set and $f, g: X \to X$ be two functions. Finally, let \(\{y_1, y_2, \dots, y_m\}\) be their equaliser.

Example (Properties of the equaliser) The equaliser, $S = \mathrm{Eq}(f, g)$ can be observed to satisfy the following:

1. For all $x \in S$, $f(x) = g(x)$.
2. For all $T \subseteq X$, such that $\forall t \in T, f(t) = g(t)$, $T \subseteq S$.

The idea is to now shift our attention to a function, rather than a set. Consider a function $h: A \to X$, where $A$ is any set. We will restrict our attention to all such functions, that satisfy the first property we outlined. To that, choose $h$ such that $f(x) = g(x)$, for all $x \in h(A)$. Lots of functions satisfy this property. Namely, the annoying case of the map $S \mapsto \emptyset$, but define only a proper subset of the equaliser. To amend this, first notice that we can rewrite the above condition, to the following, which is perhaps more enlightening. Indeed, choose $h$ such that if $h(A) \subseteq \mathrm{Eq}(f, g)$, then $f \circ h = g \circ h$. Another “problematic” candidate that arises now is the following function, $\mathrm{sequence}: \mathbb{Z} \to X$.

\[\mathrm{sequence}(k) = \begin{cases} y_1,\; k \equiv 1 \pmod m \\ y_2,\; k \equiv 2 \pmod m \\ \vdots \\ y_m, \; k \equiv 0 \pmod m \end{cases}\]

This function is a bad candidate, in the sense that it provides too much unnecessary information. In order to exclude this particular function, we may also postulate that $h$ be injective. Equivalently, we want $h(A)$ to be isomorphic to $Eq(f, g)$. The categorical weapons can now be swung in full force.

Definition (Set equaliser) Consider sets $X$ and $Y$, functions $f: X \to Y$ and $g: X → Y$. The equaliser of $f$ and $g$ is the tuple $(E, \mathrm{eq}: E \to X)$, with $f \circ \mathrm{eq} = g \circ \mathrm{eq}$, such that for any other set $Z$ and function $m : Z \to X$ with $f \circ m = g \circ m$, there exists a unique function $u: Z \to E$ with $m = \mathrm{eq} \circ u$.

That is, of course, any other potential candidate $m$ factorizes into $\mathrm{eq}$ in a unique way. For the example of the $\mathrm{sequence}$ function, we could simply take $u$ to be the $\mathrm{mod}_n$ function, defined by $(\mathbb{Z} \to \mathbb{Z}, x \mapsto x\;\mathrm{mod}\;n)$. This hopefully illustrates how $\mathrm{eq}$ is the “best” such function, in the sense that any other function can be “broken up” into $\mathrm{eq}$ and something simpler.

xkcd 895: Teaching physics. Sometimes it's better to ignore some small technical details in exposition.

The universal property in category theory, as we can now see, shows us in a precise way that which makes a definition of an object unique. We don’t have to mention $\mathrm{Eq}$ being the “largest subset” that satisfies some property, the inclusion property, or even subsets at all for that matter. Categories allow us to remove ourselves from the context and focus only on the big picture. Similar considerations can be made for all sorts of different constructions. For example, the product of two structures, the tensor algebra, and the field of the real numbers can all be characterised by universal properties.

Applied category theory?!

Decades after the very successful application of category theory to algebraic geometry and related disciplines by Grothendieck, a slow movement commenced in the theoretical sciences, a “race” of sorts to make everything categorical. Categorical quantum mechanics and Univalent foundations being the most well known. Homotopy Type Theory, an instance of category theory revealing some “unexpected links” between topology and type theory, is a contending foundation for the whole of mathematics. Outside of the pure mathematical realm, the categorical dogma has been invoked in various computer science disciplines, most recently and notably, that of machine learning and neural transformers.

But, b-but, category theory posits no non-trivial results!

Okay, I mean, neither does Shannon’s A mathematical theory of communication, but as a document it is considered foundational for computer science. “Abstract nonsense” does have its place within mathematics, where it can be used to unify and solidify many of its foundations. Barring that, do you believe that you could ever come up with the Yoneda lemma on your own?